1. مقدمة في تحليل الانحدار

تحليل الانحدار هو الطريقة الإحصائية لدراسة هذه العلاقة بين متغيرين أحدهما مستقل والاخر تابع. يعتبر الشكل الأولي للانحدار الخطي هو طريقة المربعات الصغرى التي نشرها Legendre في عام 1805، و Gauss في عام 1809. قد تعود كلمة “الانحدار” وطرق دراسة العلاقات بين متغيرين إلى حوالي 100 عام مضت. وقد تم تقديمه لأول مرة من قبل Francis Galton في عام 1886 (Bates and Watts, 1988).

يتطلب الانحدار الخطي أن يكون النموذج خطيًا في معالم نموذج الانحدار. ويشار إلى تقدير المربعات الصغرى بناءً على هذه الافتراضات باسم المربعات الصغرى العادية. في حين أن افتراضات الاستقلال والتباين المشترك صحيحة، فإن مقدرات المربعات الصغرى لها الخاصية المرغوبة لكونها أفضل مقدر خطي غير متحيز (Best Linear Unbiased Estimator (BLUE)) مع الحد الأدنى من التباين بين جميع المقدرين الخطيين غير المتحيزين المحتملين. عند استيفاء افتراض التبعية للتوزيع الطبيعي للاخطاء، فإن مقدرات المربعات الصغرى تعادل مقدرات التقدير بواسطة طريقة الامكان الاعظم (Agresti, 2002).

أربعة من مجالات المشاكل الرئيسية في تحليل المربعات الصغرى تتعلق بفشل الافتراضات الأساسية، وهي: مشكلة عدم التبعية الاخطاء للتوزيع الطبيعي (Non-normality Problem)، مشكلة عدم تجانس التباين (Heterogeneous Variances Problem)، مشكلة الارتباط الذاتي (Correlated Errors Problem)، مشكلة التعدد الخطي ( Multi-Col-linearity Problem) (Baltagi, 2001).

1.1 مشكلة التعدد الخطي

مصفوفة X التي تحتوي على المتغيرات التوضيحية قد تنتج عند اجراء عملية حسابية عليها قيم مفردة (Singularity). يحدث هذا عندما تكون بعض المجموعات الخطية لأعمدة X مساوية تمامًا للصفر. يصبح الأمر أكثر وضوحًا عندما يتم حساب تحليل المربعات الصغرى لأن الحل الفريد لـ غير موجود. تُعرف الصعوبات التي تنشأ من كون X مفردًا تقريبًا باسم مشكلة التعدد الخطي.

2.1 مشكلة التعدد الخطي في نماذج الانحدار الخطي

تذكر أن مشكلة التعدد الخطي في نماذج الانحدار الخطي تنشأ عندما تكون مجموعة خطية واحدة على الأقل من المتغيرات التوضيحية تساوي الصفر تقريبًا. هناك عدة طرق لظهور التفرد القريب (near-singularity) :

1. النموذج الرياضي السيئ الذي يضع قيودًا على المتغيرات التوضيحية التي بدورها تجبر على الالتزام بها أضافة إلى ثابت سيؤدي حتما إلى إنشاء علاقة التعدد خطي.

2. قد تظهر المتغيرات التوضيحية للتطبيق تبعية شبه خطية بسبب القيود البيولوجية أو الفيزيائية أو الكيميائية.

3. قد يؤدي عدم كفاية حجم العينة إلى إنشاء بيانات تكون فيها التبعية شبه الخطية نتيجة لعملية جمع البيانات (. (Yan and Su, 2005

ليس من السهل تحديد أصل مشكلة التعدد الخطي بوضوح ولكن من المهم للغاية فهم طبيعتها قدر الإمكان. بعد معرفة طبيعة مشكلة التعدد الخطي، سيساعدنا دائمًا تحديد مصدرها، وبالتالي العثور على الطرق المناسبة للتعامل مع المشكلة وتفسير نتائج الانحدار.

1.2.1 مقدمة إلى الانحدار المتحيز

ومن المعروف أن معاملات الانحدار التي يتم الحصول عليها باستخدام طريقة المربعات الصغرى الاعتيادية هي أفضل المقدرات الخطية الغير المتحيزة (BLUE). على وجه الدقة، فإن مقدرات المربعات الصغرى لديها أصغر تباين بين جميع المقدرات المحتملة التي تمثل الدوال الخطية للبيانات وغير متحيزة بالنسبة للمعالم التي يتم تقديرها. يعتبر متوسط مربع الخطأ (MSE) أفضل مقياس لحساب متوسط “مدي قرب” المقدر من المعلمة التي يتم تقديرها.

إذا كان مقدرًا متحيزًا يملك متوسط مربع خطأ أصغر من المقدر غير المتحيز 𝜃، فيمكن تعريف متوسط مربع الخطأ لـ على النحو التالي

(1) () MSE=

تذكر أن تباين المقدر يمكن أيضًا تعريفه على أنه

Var ( = (2)

وهذا يعني أن متوسط مربع الخطأ (MSE) يقوم بحساب متوسط الانحراف المربع للمقدر عن المعلمة التي يتم تقديرها، في حين أن التباين يحسب بواسطة متوسط الانحراف المربع للمقدر عن القيمة المتوقعة له.

إذا كان المقدر غير متحيز، فإن E()=θ و.MSE() =( إذا كان المقدر متحيزًا، فإن MSE تساوي تباين المقدر بالإضافة إلى مربع انحيازه، حيث Bias () = . من الممكن جدًا أن يحصل المقدر المتحيز على تباين أصغر بدرجة كافية من تباين المقدر غير المتحيز من أجل التعويض عن التحيز المقدم.

في مثل هذه الحالات، يكون المقدر المتحيز أقرب في المتوسط إلى المعلمة المراد تقديرها من المقدر الغير المتحيز. ويمثل ذلك الاستراتيجية الرئيسية لتكتيكات الانحدار المتحيز (Hoerl and Kennard, 1975).

الشكل (1) رسم توضيحي لتقدير الانحدار المتحيز

يستعرض الشكل 1 الميزات المحتملة للمقدرين المتحيزين. يتم تمثيل التوزيع الاحتمالي لمقدر غير متحيز θ̃ بالنسبة للمعلمة بالمنحنى العادي المتمركز عند E(θ̃) . لاحظ أن التحيز هو الفرق بين (E(θ̃ وθ. لاحظ أيضًا أن الفارق الأصغر في هذا التوزيع يعكس تباينه الأصغر. ولذلك، قد يكون من الممكن العثور على مقدر يكون مجموع انحيازه التربيعي وتباينه (أي MSE) أصغر من تباين المقدر غير المتحيز.

2.2.1 الدراسات السابقة

تم اقتراح العديد من طرق الانحدار المتحيزة كحلول لمشكلة التعدد الخطي. انكماش Stein (Stein, 1960) وانحدار انكماش ريدج (Hoerl and Kennard, 1975) ومشغل الانكماش والاختيار المطلق الأقل (LASSO) الذي اقترحه Tibshirani (1996)، وانحدار المكونات الرئيسية Hocking ، Speed ، و Lynn (1976)، Marquardt (1970)، و Webster ، Gunst ، و Mason (1974).

لقد تم قبول طرق الانحدار المتحيزة هذه عالميًا ولكن يجب استخدامها بحذر. يوضح مبرر استخدام معيار متوسط مربع الخطأ (MSE) لأساليب الانحدار المتحيزة أن مثل هذه الأساليب يمكن أن توفر تقديرات أفضل للمعالم بمعنى المتوسط المربع. ولكنها لا تعني بالضرورة أن حل الانحدار المتحيز مقبول (أو حتى أفضل) من حل المربعات الصغرى لأغراض أخرى غير تقدير المعالم. ضع في اعتبارك أن التعدد الخطي لا يؤثر على دقة مقدر الاستجابة، فهي لا تسبب تضخم التباين في مقدرات الاستجابة في نقاط أخرى.

أن انحدار انكماش ريدج قد حظي بأكبر قدر من القبول لدي العديد من البحاث، ولهذا فقد تم استخدامه بنجاح واضح في العديد من المشاكل مختلفة. انحدار انكماش ريدج وانحدار المكونات الرئيسي هما المنافسان الوحيدان مستخدمان في طرق الانحدار المتحيزة. تذكر أن أساليب الانحدار المتحيزة تتعامل مع مشكلة التعدد الخطي عن طريق تقليص تأثيرات العلاقة الخطية المتداخلة حسابيًا.

2. مقدرات الانكماش

1.2 مقدمة

دع المتغيرات التوضيحية المستخدمة في أي دراسة معينة يتم ترتيبها في شكل مصفوفة تسمى X-matrix. يمكن صياغة الإجراءات التي سيتم عرضها في هذا البحث كامتداد مباشر لتحليل الانحدار. تختلف هذه الإجراءات في مصفوفة X المستخدمة وأيضًا كيفية تحديد تلك المصفوفة. مهما كانت المصفوفة X المستخدمة، سيكون هناك عدد متساو من معاملات الانحدار. كلما زادت القيمة المطلقة لهذه المعاملات، كلما زادت اختلاف القيم المقدرة.

إذا كان معامل الانحدار يساوي الصفر، فستكون القيم المقدرة خطًا مستقيمًا (أي موازيًا للمحور السيني، ويتم وضعه عند الوسط الغير مشروط لمتغير الاستجابة). مع زيادة معامل الانحدار، ستكون للدالة الناتجة المتدرجة أثر في زيادة الحجم. يصبح خط التقدير أقل انتظامًا. وبشكل عام، فإن احتمالية عدم الانتظام تكون أكبر مع زيادة معاملات الانحدار (Hoerl and Kennard, 1975).

تم تقديم اقتراحين شائعين لكيفية التحكم في حجم معاملات الانحدار، وهما: .

جزائية L₁: تقييد مجموع القيم المطلقة لمعاملات الانحدار ليكون أقل من بعض الثوابت C .

جزائية L₂:: تقييد مجموع معاملات الانحدار المربعة ليكون أقل من بعض الثابت C.

ومع ذلك، كلما كانت قيمة C أصغر، كان المجموع أصغر. وكلما كان المجموع أصغر، كلما كانت معاملات الانحدار أصغر في الحجم. وببساطة فأن هذان القيدان يؤديان إلى ما يسمى بطرق الانكماش، فعندما يتم تقليص معاملات الانحدار نحو الصفر، يجعل القيم المقدرة أكثر تجانسًا. ولذلك، فإن الهدف الرئيسي هو إدخال قدر صغير من التحيز في معاملات الانحدار المحسوبة في اجل المقايضة للحصول على قدر كبير من التخفيض في تباينها.

يتم تطبيق الانكماش على تقديرات الانحدار المعتادة لهدفين:

أولا، للمهتمين في اختيار النموذج. وبالتالي، يمكن لأقل مشغل الانكماش والاختيار مطلقًا (Least Absolute Shrinkage and Selection Operator) LASSO توفير بدائل مفيدة لإجراءات اختيار النموذج المعتادة.

ثانياً، المهتمون بتحقيق توازن جيد بين التحيز والتباين. وبالتالي، يمكن لمقدر انحدار ريدج (Ridge ) الانكماشي أن يوفر بدائل مفيدة لمعالجة مقايضة التحيز والتباين في تحليل الانحدار المعتاد (Baltagi, 2001).

2.2 مقدمة في انحدار ريدج (Ridge Regression)

بشكل عام، يعتبر انحدار ريدج الانكماشي (ٌRidge Shrinkage) أحد التدابير العلاجية الأكثر استخدامًا للتعامل مع مشكلة التعدد الخطي عند استخدام تقدير المربعات الصغرى الاعتيادية.

مشكلة التعدد الخطي تحدث عندما تكون المتغيرات التوضيحية المضمنة في النموذج الخطي مرتبطة بشكل كبير مع بعضها البعض. عندما يحدث هذا، فإن المصفوفة X^t X تميل إلى إنتاج القيمة الشاذة. ونتيجة لذلك، فإن تحديد تقديرات المربعات الصغرى سيواجه بالتأكيد مشاكل عددية. انحدار انكماش ريدج (Ridge Shrinkage) هو نوع مقيد من المربعات الصغرى. إنه يحل مشكلة التقدير من خلال إنتاج مقدر متحيز، مع وجود تباينات صغيرة (Weisberg 2005)

1.2.2 التطوير النظري لمقدر انكماش ريدج

بالنسبة لأي مقدر للمربعات الصغرى b، يمكن إعادة كتابة معيار المربعات الصغرى كحد أدنى، حيث تم الوصول إليه عند . الصيغة التربيعية في b

Q(b) = Q(b) =

= +

= (3)

كنتورات كل ثابت من الصيغة التربيعية هي أشكال hyperellipsoids تتمركز عند مقدر المربعات الصغرى الاعتيادي . ومن المعقول أن نتوقع من (3) أنه إذا تحرك المرء بعيدًا عن Q_min، فإن الحركة تكون في اتجاه يقصر الطول من b.

في انحدار انكماش ريدج Ridge Shrinkage Regression، يمكن تحديد مشكلة التحسين على النحو التالي

minimizing مع مراعاة = (4)

بالنسبة لبعض الثوابت ϕ₀. يضمن القيد المفروض وجود مجموع من البواقي صغيرة بشكل معقول من المربعات Q(β) عند مقارنتها بالحد الأدنى Q_min. يعرض الشكل 2 محيط المجموع البواقي للمربعات مع قيد انكماش الريدج L₂ في الحالة ثنائية الأبعاد (Kotz, 2004 and Nadarajah)

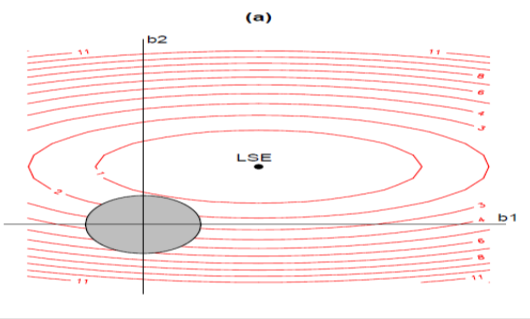
الشكل (2) كنتورات مجموع مربعات البواقي والقيود في انحدار انكماش ريدج Ridge Shrinkage

ومن وجهة نظر مشكلة لاغرانج (Lagrangian)، فهي تعادل التقليل

(5)

حيث k هو عامل الانحراف المختار لاستفاء متطلبات القيد.

ولذلك، قم بالتمييز بين Q* (β) فيما يتعلق بـ β

(∂() (6)

الذي ينتج مقدر انكماش ريدج Ridge Shrinkage على النحو التالي

= (7)

هناك طريقة بديلة تتمثل في توضيح مشكلة انكماش ريدج Ridge Shrinkage في شكل المربعات الصغرى المقيدة بواسطة

minimizing

لبعض القيمة الثابتة لـ s.

ومن هنا تصبح مشكلة لاغرانج (Lagrangian) مجرد التقليل من ذلك

الذي ينتج نفس المقدر الوارد في (7) تتحكم معلمة العقوبة λ ≥ 0 في مقدار الانكماش في . كلما زادت قيمة λ كلما زاد مقدار الانكماش. لهذا السبب، فإن مقدر انكماش ريدج يسمى في كثير من الأحيان مقدر الانكماش (Bates and Watts, 1988).

3.2  لاسو LASSO: أقل عامل انكماش واختيار مطلق 

(least absolute shrinkage and selection operator) LASSO

يعتبر عامل الانكماش والاختيار الأقل المطلق (LASSO) طريقة انكماش أخرى مثل انحدار انكماش ريدج، ولكن مع ميزة مهمة وجذابة في الاختيار المتغير. بدلاً من ذلك، فإن انحدار انكماش ريدج يجعل عملية الاختيار مستمرة من خلال تغيير معلمة الانكماش k وبالتالي تصبح أكثر استقرارًا. من خلال هذه العملية، لا يضع انحدار انكماش ريدج أي معاملات على الصفر، لأنه لا يعطي نموذجًا يمكن تفسيره بسهولة كما هو الحال في اختيار المجموعات الفرعيةsubset selection ( Greene, 2000).

تم اقتراح تكتيك LASSO للحفاظ على مزايا اختيار المجموعات الفرعية وانحدار انكماش ريدج عن طريق تقليص بعض المعاملات نموذج الانحدار وضبط المعاملات نموذج الانحدار الأخرى على الصفر. يتم الحصول على مقدر LASSO لـ β بواسطة

minimizing ..

وبشكل أكثر وضوحًا، يتم استبدال (L₂ بجزاء ) في انحدار انكماش ريدج بـ L₁ بجزاء في LASSO. إذا تم اختيار s لتكون أكبر من أو تساوي ، فإن تقديرات LASSO هي تمامًا نفس تقدير المربعات الصغرى. إذا تم اختيار s لتكون أصغر من، فسوف يتسبب ذلك في انكماش الحلول نحو الصفر.

يعرض الشكل 3 كنتورات مجموع مربعات البواقي مع قيد L₁ LASSO في الحالة ثنائية الأبعاد (Greene, 2000)

الشكل (3) كنتورات مجموع مربعات البواقي ودوال القيود في LASSO.

تجدر الإشارة إلى أنه في الشكل 2، منطقة القيد في انحدار انكماش ريدج Ridge Shrinkage Regression لها شكل قرص. بينما في الشكل 3، منطقة القيد في LASSO لها شكل ماسي. يمكن ملاحظة أن كلاً من طريقتي انحدار انكماش ريدج Ridge Shrinkage Regression و LASSO تبدأ بإيجاد النقطة الأولى التي تصطدم فيها الخطوط البيضاوية بمنطقة القيد. ولكن، على عكس حالة القرص Ridge Shrinkage Regression، فإن الماسة الموجودة في LASSO بها زوايا. إذا حدث الحل عند زاوية، فإن معامله يساوي الصفر. ويمكن أيضًا ملاحظة أن حل LASSO يتنافس مع حل انحدار انكماش ريدجRidge Shrinkage Regression ولكن مع العديد من تقديرات المعاملات نموذج الانحدار الصفرية. في حالة التصميمات المتعامدة حيث = I، يمكن كتابة مقدر LASSO كـ

= sign₊ (8)

حيث يتم تحديد γ بواسطة الشرط

لقد قارنا أداء انحدار انكماش ريدج Ridge Shrinkage Regression و LASSO في سياق أكبر. الاهتمام الرئيسي في هذا البحث هو أنماط الانكماش مع تغير λ. يميل انحدار انكماش ريدج إلى تقليص معاملات نموذج الانحدار بحيث تصل جميعها إلى الصفر معًا عندما تصبح λ كبيرة. يقوم LASSO بتقليص المعاملات بحيث يصل بعضها إلى الصفر قبل البعض الآخر عندما تصبح λ كبيرة (Hastie et al., 2002).

4.2 مقدر LASSO التكيفي

دعونا نفكر في انحدار LASSO المرجح

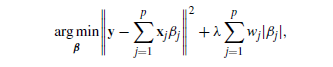(9)

حيث wj هو ناقل أوزان معروف. إذا كانت الأوزان تعتمد على البيانات وتم اختيارها بعناية، فيمكن أن تحتوي LASSO الموزونة على خصائص Oracle.

تسمى المنهجية الجديدة انحدار LASSO التكيفي (ALASSO).

1.4.2 تعريف انحدار LASSO التكيفي

^˄

لنفترض أن β هو مقدر الجذر n المتسق لـ β؛ على سبيل المثال، يمكننا استخدام β (باستخدام OLS). اختر ، وحدد متجه الوزن w_j\=1/ |β_j|.

يتم إعطاء Adaptive LASSO المستخدم لتقدير β بواسطة

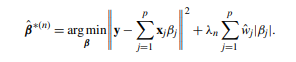(10)

وبالمثل، دع j: where β_jⁿ A_n [تجدر الإشارة إلى أن β^*n هي مشكلة تحسين محدبة، وبالتالي فهي لا تعاني من مشكلة الحد الأدنى المحلي المتعددة، ويمكن حل أداة التصغير العالمية الخاصة بها بكفاءة (على سبيل المثال

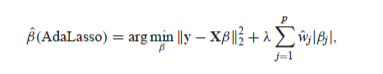
وهذا يختلف تمامًا عن عقوبات أوراكل المقعرة. يعد Adaptive LASSO في الأساس طريقة معاقبة المستوى الأول. يمكننا استخدام الخوارزميات الفعالة الحالية لحل LASSO لحساب تقديرات LASSO التكيفية.

Zou (2006) في ورقته المهمة بعنوان “The Adaptive Lasso وخصائص أوراكل الخاصة بها”. تبين أنه مع الاختيار الصحيح ل، _نيتمتع Adaptive LASSO بالتأكيد بخصائص Oracle.

5.2 مقدر الشبكة المرنة Elastic Net Estimator

يعد انحدار الشبكة المرنة Elastic Net(ENET) خوارزمية قوية للتعلم الآلي تجمع بين ميزات كل من LASSO وRidge Regression. إنها تقنية انحدار منتظمة تُستخدم للتعامل مع مشكلات الخطية المتعددة والملاءمة الزائدة، والتي تعتبر شائعة في مجموعات البيانات عالية الأبعاد. تعمل هذه الخوارزمية عن طريق إضافة مصطلح عقوبة إلى المعيار. وظيفة المربعات الصغرى الهدف. في هذا القسم الفرعي التالي، سنقدم انحدار الشبكة المرنة (ENET) بمزيد من التفاصيل، بالإضافة إلى مزاياه وعيوبه.

1.5.2 نظرة عامة على الانحدار الصافي المرن

تم تقديم انحدار الشبكة المرنة (ENET) بواسطة ( Zou and Hastie )2005 إنها خوارزمية انحدار خطي تضيف شرطين جزائيين إلى دالة الهدف القياسية ذات المربعات الصغرى. هذين الحدين الجزائيين هما معايير L1 وL2 لمتجه المعامل، والتي يتم ضربها بمعلمتين مفرطتين γ و λ. يتم استخدام معيار L1 لأداء ميزة الاختيار، في حين يتم استخدام معيار L2 لأداء ميزة التخفيض.

يمكن تمثيل نموذج انحدار الشبكة المرنة (ENET) على النحو التالي:

y = b₀ + b₁ x₁ + b₂ x₂+………. + b_n x_n + ε

حيث y هو المتغير التابع، b₀ وهو التقاطع، وb₁،….,b_n هي معاملات الانحدار، وx₁،….,x_n هي المتغيرات المستقلة، وε هو مصطلح الخطأ. يحاول نموذج انحدار الشبكة المرنة (ENET) تقليل الوظيفة الهدف التالية:

[ RSS + ]( 1-² + a ¹[

حيث RSS هو مجموع المربعات المتبقية، ومعلمة التنظيم، ، هو ناقل المعامل، وهو معلمة الخلط بين L₁ وL₂، والقواعد،² هو المعيار L₂ لـ و¹ هو معيار L₁ لـ .

مجموعة البيانات المحددة ( )، وحدد البيانات المصطنعة بواسطة

x* _{(n + p ) xp} *_{(n + p )} ( ).

بالتعويض في المعادلة (9) ينتج ما يلي

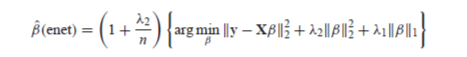
من المهم ملاحظة أنه في انحدار Elastic Net، يتم ضبط الإعداد = صفر ينتج عنها حل انحدار Ridge =1 ينتج عنها حل LASSO. أثناء الإعداد عقوبة مختلطة تمثل مزيجًا خالصًا من مقدرات انحدار Ridge وLASSO.

بالإضافة إلى ذلك، يؤدي ضبط إلى إنتاج حل OLS. ولذلك توفر الشبكة المرنة (ENET) إطارًا مرنًا من خلال إجراءات Ridge وLASSO المنتظمة

(انظر Rish and Grabarnik, 2015, Helwig, 2017).

يمكن رؤية هذه الميزات المثيرة للاهتمام بوضوح في شكل 4 (Helwig, 2017).

الشكل (4) المخططات الكنتورية لمقدرات الانحدار Ridge و LASSO و Elastic Net

يوضح الشكل 4 مدى ملاءمة هندسة مخططات الكنتور لكل من انحدار Ridge و LASSO و Elastic Net في الإحداثيات ثنائية الأبعاد، حيث تكون الزوايا الحادة عند القمم والحواف ومحدبة تمامًا وقوة التحدب التي تختلف مع قيمة .

6.2 مقدر الشبكة المرنة التكيفي Adaptive Elastic Net Estimator

تذكر أن Elastic Net Regression ينتج نماذج انحدار خطي بسيطة أو متعددة يتم تغطيتها بأسلوب L1 وL2-norm. والنتيجة هي تقليل المعاملات بشكل فعال كما هو الحال في انحدار Ridge مع عقوبة التخفيض λ₂ P₂ (B)) وتعيين بعض المعاملات إلى الصفر كما هو الحال في انحدار LASSO مع عقوبة التخفيض λ₁P₁ (B) Zou and Hastie, 2005).

يمكن ضبط مقدار العقوبة بشكل جيد باستخدام الثوابت (λ₂ , λ₁ ). وبشكل أكثر تحديدًا، يقلل انحدار الشبكة المرنة التكيفية (AENET) من المربعات الصغرى المعاقب عليها (PLS) أو الدالة الهدف

Β_AENET (11)

لاحظ ( Tibshirani )1996 أن الأداء التنبؤي التجريبي لـ LASSO يهيمن عليه انحدار Ridge (أي الانحدار الخطي المنتظم L2) عندما تكون المتغيرات المستقلة مرتبطة بشكل كبير، في حين ينعكس الوضع عندما يكون هناك عدد صغير نسبيًا من أكثر المتغيرات المستقلة.

لذلك، قد يكون من الضروري الجمع بين معياري L1 وL2 لتحقيق “الأفضل في كل من ميزات انحدار Ridge وLASSO.

بافتراض ان

تصبح المربعات الصغرى المعاقب عليها (PLS) أو الدالة الموضوعية للشبكة المرنة التكيفية (AENET) باستخدام المعادلة (12) كما يلي:

حيث ان هي معلمة العقوبة (أو الضبط) لانحدار الشبكة المرنة التكيفية (AENET) و هي معلمة الخلط وتتحكم في تأثير L1 وL2 التي تعاقب عليه ( Xiao and Xu, 2015).

تتمتع كل من تقديرات LASSO وElastic Net بمعاملات كبيرة غير صفرية مع انحياز مقارب لا يمكن تجاهله، ولحل هذه المشكلة، اقترح Zou (2006) مقدر LASSO التكيفي التالي (ALASSO)

 

حيث w_j هي معلمة ترجيح تعتمد على البيانات، والتي يمكن تقديرها بواسطة w_j = ( |β_jⁱⁿⁱ |^−γ ) و γ هو ثابت موجب. βⁱⁿⁱ عبارة عن مجموعة من المعلمات الأولية، والتي يمكن حسابها بواسطة المربعات الصغرى العادية (OLS) أو انحدار Ridge.

يمكن النظر إلى الشبكة المرنة التكيفية (AENET) على أنها مزيج من الشبكة المرنة (ENET) وانحدار LASSO التكيفي (ALASSO).

سنقوم أولاً بحساب تقدير الشبكة المرنة) Elastic Net ENET) المحددة كما في السابق، ثم نقوم ببناء الأوزان التكيفية بواسطة

(15)

حيث γ لا يزال ثابتًا موجبًا. للحصول على تقدير الشبكة المرنة التكيفية (AENET)، سنحل مشكلة التحسين التالية:

(16)

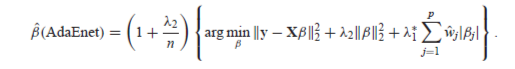
تضمن الشبكة المرنة التكيفية) Adaptive Elastic Net AENET) أيضًا اتساق الاختيار المتغير وخصائص الحالة الطبيعية المقاربة مثل Adaptive LASSO ) ALASSO) ويمكنها التعامل مع مشكلة التعدد الخطي عن طريق إضافة شروط تنظيم L2.

3. دراسة المحاكاة

1.3 مقدمة

تم تخصيص هذا الفصل لمقارنة أداء المقدرات الخمسة المقترحة: وهي: ريدج (Ridge)، واللاسو (Lasso)، والشبكة المرنة (ُElastic Net)، واللاسو التكيفي (Adaptive Lasso)، ومقدرات الشبكة المرنة التكيفية (Adaptive Elastic Net) التي استخدمت في معالجة مشكلة التعدد الخطي ومشكلة تعدد الابعاد عبر المحاكاة. من أجل التعرف بشكل أفضل على خصائص مقدرات الانحدار الجزائية وبعض بدائله، قمنا بحساب مجموعتين من المحاكاة. يتم وصف الإجراءات الدقيقة في القسم التالي. تتضمن عمليات المحاكاة العديد من تقديرات الانحدار الجزائية. لقد قمنا بتضمين نهج OLS ذي الصلة على الرغم من حقيقة أنه يُستخدم بشكل أساسي لتقدير النموذج عندما لا يكون مشكلة تعدد الابعاد موجودة.

بشكل عام، دراسات المحاكاة هي في الغالب تقنية لإجراء تجارب على نموذج. على عكس الطرق التحليلية؛ عمليات المحاكاة دقيقة وسهلة الفهم ولكن فقط في حالة استخدامها بشكل مناسب. في هذه الأطروحة، تستخدم المحاكاة أجهزة الكمبيوتر التي يتم إنشاؤها كمتغيرات اصطناعية بدلاً من البيانات الحقيقية. يمكن استخدام هذه البيانات الاصطناعية تمامًا مثل البيانات الحقيقية لإنتاج على سبيل المثال المتغيرات المستقلة والتابعة ومقارنة نتائج المقدرات المقترحة نظرًا لأن البيانات الاصطناعية تحت سيطرة الباحث، وغالبًا ما يكون الأداء النظري الإحصائي معروفًا. تم إجراء جميع الحسابات والرسومات في هذه الأطروحة باستخدام حزمة البرامج R، والتي تعتمد على اللغة الإحصائيةR

(R Language and environment for Statistical computing, 2015).

ومع ذلك، لدينا ثقة في نتائجنا التي تعد مفيدة جدًا في تقييم الأداء العملي للمقدرات الخمسة المقترحة في هذه الدراسة التي نستخدمهن لحل مشكلة التعدد الخطي و مشكلة تعدد الابعاد.

2.3 وصف تجربة المحاكاة

في دراسة المحاكاة هذه، تمت مقارنة تقديرات الانحدار الجزائية الخمسة المقترحة مع بعضها البعض باستخدام خيارات مختلفة من الارتباط ρ = (0.00 و 0.10 و 0.25 و 0.50 و 0.75 و 0.90) بين المتغيرات التوضيحية. وقد تم القيام بذلك من أجل تحديد بعض المزايا الشائعة لمقدرات الانحدار الجزائية التي يتم الاستشهاد بها بشكل أفضل، مثل أيها يعمل بشكل أفضل عندما تكون المتغيرات التوضيحية في نموذج الانحدار مترابطة بقوة. تم تصنيف الدراسة إلى نمطين مختلفين كالتالي:

النمط 1: توزيع حد الخطأ يتبع التوزيع طبيعي،

النمط 2: توزيع حد الخطأ لا يتبع التوزيع طبيعي.

في كل نمط، عدة اختيارات لعدد المتغيرات التوضيحية P = (20 و50 و100). كانت أحجام العينة n التي تم النظر فيها صغيرة الحجم ومتوسط الحجم وكبير الحجم وكان النموذج على شكل Y.

أخيرًا، تم استخدام نوعين مختلفين من التوزيعات الهامشية بالنسبة لحد خطأ هامشين هما: التوزيع الطبيعي Normal distribution.، وتوزيع (3)t (Heavy tailed t-distribution) .

1.2.3 الملخص العددي والرسومات البيانية

باستعمال خيارات مختلفة من معاملات الارتباطات ρ = (0.00 و0.10 و0.25 و0.50 و0.75 و0.90) بين المتغيرات التوضيحية وثلاثة أحجام العينات الصغيرة (n = 10 و14 و18) عندما يتم تحديد عدد المتغيرات المستقلة بـ 20. بالنسبة لأحجام العينة المتوسطة (n = 20 و30 و40) عندما يتم تحديد عدد المتغيرات المستقلة بـ 50. بالنسبة لأحجام العينات الكبيرة (n = 60 و70 و80) عندما يتم تحديد عدد المتغيرات المستقلة بـ 100 وكذلك توزيعات الأخطاء الهامشية المختلفة لكل 1000 عملية محاكاة مختلفة بشكل مستقل، يعطي كل منها النتائج المبينة في مخططات الصندوق (شكل 3 وشكل 4). نتائج المتوسطات ونتائج الانحرافات المعيارية لمتوسط ​​الخطأ التربيعي (MSE) الذي تم الحصول عليه من خلال استخدام المقدرات الستة المقترحة في هذه الدراسة.

تجربة المحاكاة الاولي: حد الخطاء يتبع التوزيع الطبيعي

الشكل (5) يوضح مخططات الصندوق لكيفه تتأثر خيارات معاملات الارتباط المختلفة على المتوسط ​​(الانحراف المعياري) لقيمة MSE للمقدرات الستة المقترحة (OLS و Ridge و Lasso و Elastic Net و Adaptive Lasso و Adaptive Elastic Net) , 50 , 100 p = 20 من خلال نمط 1.

تجربة المحاكاة الثانية: حد الخطاء لا يتبع التوزيع الطبيعي

الشكل (6) يوضح مخططات الصندوق لكيفه تتأثر خيارات معاملات الارتباط المختلفة على المتوسط ​​(الانحراف المعياري) لقيمة MSE للمقدرات الستة المقترحة (OLS و Ridge و Lasso و Elastic Net و Adaptive Lasso و Adaptive Elastic Net) , 50 , 100 p = 20 من خلال نمط 2.

4. مناقشة دراسة المحاكاة

الغرض من هذا القسم هو تلخيص فعالية التقدير والاتساق بين مقدرات Ridge وLASSO وElastic Net وAdaptive Lasso وAdaptive Elastic Net التي يتم استخدامها للتعامل مع مشكلة “التعدد الخطي” ومشكلة “تعدد الابعاد” وحلها عندما تكون الأخطاء إما موزعة بشكل طبيعي أو موزعة بشكل غير طبيعي.

1.4 النمط الأول: حد الخطأ موزع توزيعاً طبيعياً

في دراسة المحاكاة الأولى، تم التخطيط في حالة وجود مشكلة التعدد الخطي ومشكلة تعدد الابعاد بين المتغيرات التوضيحية من خلال استخدام ستة مقدرات (OLS، Ridge، LASSO، Elastic Net، Adaptive Lasso، (Adaptive Elastic Net وتم إجراء المقارنات فيما بينها باستخدام القيم المتوسطة لـ (MSE) بالإضافة إلى قيم الانحرافات المعيارية المقابلة لها على افتراض أن حدود الخطأ موزعة بشكل طبيعي. تم التوصل إلى النقاط الثلاث المثيرة للاهتمام التالية:

1- يعطي مقدرOLS دائما قيم MSE كبيرة جدًا بسبب وجود مشكلة التعدد الخطي.

2- يعتبر انحدار ريدج Ridge أحد أكثر إجراءات التقدير شيوعًا، على الرغم من الجدل حوله، لحل مشكلة العلاقات الخطية المتعددة. تندرج الإجراءات التي تمت مناقشتها في هذه المحاكاة ضمن نوع تقنيات التقدير المتحيزة. وهي تستند إلى هذه الفكرة: على الرغم من أن مقدر OLS يعطي أفضل مقدر خطي غير متحيز (Blue)، إلا أنه لا يوجد حد أعلى لتباين المقدر وقد يؤدي وجود علاقة خطية متعددة إلى إنتاج تباين كبير. لذلك، يمكن للمرء أن يتصور أنه، في ظل شرط التعددية الخطية، يجب دفع ثمن باهظ مقابل خاصية عدم التحيز التي ينجزها الباحث باستخدام انحدار ريدج Ridge يتم استخدام التقدير المتحيز لتحقيق انخفاض كبير في التباين مع زيادة مصاحبة في استقرار معاملات الانحدار. تصبح المعاملات متحيزة ويكون انخفاض التباين أكبر من التحيز الذي يحدث في المقدرات.

3- وقد لوحظ، بغض النظر عن الزيادة في حجم العينة n 80 ,70 ,60 =أو زيادة معامل الارتباط ρ، في جميع الحالات عند 20= p و50 و100، يحتفظ مقدر انحدار ريدج Ridge بالمركز الأول ويتبعه في المركز الثاني مقدر الشبكة المرنة التكيفية .Adaptive Elastic Net

4- في حين أن مقدرات اختيار النموذج الثلاثة الأخرى: LASSO، وAdaptive LASSO، وElastic Net تؤدي أداءً جيدًا للغاية في إزالة مشكلة الخطية المتعددة ومشكلة تعدد الابعاد، إلا أنها تتمتع بدقة تنبؤ أقل.

2.4 النمط الثاني: حد الخطأ غير موزع توزيعاً طبيعياً

أما في دراسة المحاكاة الثانية فقد افترض أن الأخطاء توزعت وفق توزيع t ثقيل الذيل (التوزيع غير الطبيعي). تم إجراء جميع الإعدادات الأخرى كما في دراسة المحاكاة الأولى. تم التوصل إلى النقاط الثلاث التالية المثيرة للاهتمام:

1- استمرار مقدر OLS في إعطاء قيم MSE كبيرة جدًا بسبب وجود مشكلة الخطية المتعددة.

2- مع زيادة حجم العينة n 80 ,70 ,60 =، يلاحظ أن المقدر في المقام الأول هو مقدر انحدار ريدج Ridge، يليه في المركز الثاني مقدر Elastic netثم في المركز الثالث مقدران متساويان تقريبًا في الاحتمال، وهما مقدر Adaptive Elastic Net و Lasso وهذا الاخير محتمل أيضًا في حالة العينات الصغيرة عندما عدد المتغيرات p= 20.

3- لوحظ أنه في حالة النمط الثاني، بغض النظر عن حجم العينة n 40 ,30 ,20 =وعدد المتغيرات p=50، فإن مقدر الشبكة المرنة التكيفية Adaptive Elastic Net يعمل بشكل أفضل وهو يأتي بعد ذلك مقدر انحدار ريدج Ridge.

لمقارنة تأثير تبعية حد الخطأ الي التوزيع الطبيعي الناتجة عن التغيير من النمط 1 إلى النمط 2:

1- ويلاحظ بغض النظر عن نوع توزيع حد الخطأ، فإذا كان عدد المتغيرات يساوي p=20,50,100، هناك اتفاق حول المقدر الذي يحتل المركز الأول وهو مقدر انحدار ريدج Ridge. بينما المركز الثاني يكون لمقدر الشبكة المرنة التكيفية Adaptive Elastic Net ومع ذلك، هناك اختلاف في المقدر الذي يحتل المركز الثالث، حيث يلاحظ أنه يتأرجح بين المقدر Lasso والمقدر Elastic net عند بعض القيم.

• أثبت الخمسة مقدرات الانحدار الجزائية مختلفة المستخدمة في هذه الدراسة قوة مرونتها (Robustness) تجاه تبعية حد الخطأ الي التوزيع الطبيعي، حيث لم يكن هناك تأثير كبير على نتائج المحاكاة.

كتعليق أخير، أظهرت الدراسة العددية التي أجريت على بيانات المحاكاة أن قيم MSE باستخدام مقدر انحدار ريدج Ridge تميل إلى تقليل عدد المتغيرات المحددة بشكل كبير، مع الحفاظ على دقة التقدير، وهي خاصية مرغوبة في العديد من مشكلات اختيار النموذج والانحدار المتحيز في التطبيقات المختلفة في العالم الحقيقي.

لذلك، يحافظ مقدر انحدار ريدج Ridge على تفوقه على جميع المقدرات الأخرى، لأنه يعطي أصغر قيمة MSE وكذلك أصغر قيمة للانحراف المعياري بغض النظر لاختلاف معامل الارتباط ρ او عدد المتغيرات التوضيحية p او حجم العينة n. كما يحافظ مقدر Elastic netعلى المركز الثاني.

تعتبر قيمة MSE باستخدام مقدر Adaptive Elastic Net أكثر أمانًا من LASSO وAdaptive LASSO، من خلال تقديم تنظيم L₂، مما قد يؤدي إلى تجنب الحذف المتهور للمتغيرات المهمة المرتبطة، مع الحصول على متغيرات أقل تحديدًا بكثير من مقدر الشبكة المرنة التكيفية . Adaptive Elastic Net

ربما تكون هذه هي المفاضلة ضمن قيمة MSE باستخدام مقدر Adaptive Elastic Net وAdaptive LASSO في دقة التنبؤ، وبالتالي توفر لنا رؤية أكثر حول مواصلة فحص المتغيرات المستقلة المرتبطة. علاوة على ذلك، تجدر الإشارة إلى أنه من خلال تحليل المتغيرات التي تم حذفها في كل خطوة، يمكن اكتساب المزيد من المعرفة حول بنية المتغيرات المستقلة المرتبطة.

من هذه المناقشة، يمكننا أن نرى أن استخدام مقدرات Adaptive LASSO وElastic Net يعد أمرًا عمليًا تمامًا في الظروف التي يُعتقد فيها أن قيم معاملات نموذج الانحدار الكبيرة غير محتملة من وجهة نظر عملية.

وختاما، يوصى بشدة باستخدام مقدرات الانحدار الجزائية لحل مشكلات ملاءمة النموذج التي تتضمن مشكلة التعدد الخطي وتعدد الابعاد، نظرًا لوجود أدلة إيجابية كافية حول الانحدار المتحيز تشير إلى أنه يجب أن يكون جزءًا من أي تقنية لاختيار النموذج.

المراجع والمصادر

1. Agresti, Alan (2002) Categorical Data Analysis, John Wiley and Sons, USA.
2. Baltagi, B. H. (2001). “Econometric Analysis of Panel Data”. Wiley, John & Sons:New York .
3. Bates, D.M. and Watts, D.G (1988). Nonlinear Regression Analysis

and Its Applications. John Wiley and Sons, USA.

1. Galton, Francis (1886) “Regression towards mediocrity in hereditary stature.” The Journal of the Anthropological Institute of Great Britain and Ireland vol. 15: pp. 246-263.
2. Greene, W. H. (2000). Econometric Analysis, 4th Edition. Prentice.
3. Hastie, T., Tibshirani, R., and Friedman, J. (2002). The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer-Verlag, New York, NY: USA.
4. Helwig, N. E. (2017). “Adding bias to reduce variance in psychology results: A tutorial on Penalized regression”. The Quantitive Methods for Psychology, vol. 13(1) pp. 1-19.
5. Hocking, R. R., Speed, F. M., and Lynn M. J. (1976) “A Class of Biased Estimators in Linear Regression”, Technometrics vol. 18, No. 4, pp. 425-437
6. Hoerl A.E., and Kennard R.W. (1975) “Ridge regression: Biased estimation for nonorthogonal problems”. Technometrics. Vol. 12: pp 55–67.
7. Marquaridt, Donald W. (1970) “Generalized Inverses, Ridge Regression, Biased Linear Estimation, and Nonlinear Estimation” Technometrics  Vol. 12, No. 3, pp 591-612
8. R Language and environment for Statistical computing, (2015) R Foundation for statistical computing Vienna, ISBN 3-900051-07-0.
9. Rish, I. and Grabarnik, R. D. (2015). Sparse Modelling, Algorithms and Applications. First Edition, CRC Press, Taylor and Francis Group, USA.
10. Stein, C. (1960). “Efficient nonparametric testing and estimation”. In Proceedings of the Third Berkeley Symposium on Mathematical Statistics and Probability, 1954–1955, Vol. I 187–195. Univ. California Press, Berkeley and Los Angele, USA
11. Tibshirani R. (1996) “Regression shrinkage and selection via the lasso”. Journal of the Royal Statistical Society. Series B :Methodol. 1; 267–288.
12. Webster, J.T., Gunst, R. F. and Mason, R. L. (1974) “ Latent Root Regression Analysis “ Technometrics, Vol. 16, Issue 4, pp 513-522
13. Weisberg, S. (2005). Applied Linear Regression. 3^rd edition. Wiley and Sons, Inc.
14. Zou, H. (2006) “The Adaptive Lasso and Its Oracle Properties” Journal of the American Statistical Association, Theory and Methods Vol. 101, No. 476. pp 1418-1429
15. Zou H. and Hastie T. (2005) “Regularization and variable selection via the elastic net.” Journal of the Royal Statistical Society: Series B (Statist Methodol); 67:301–320.
16. Xiao, Nan and Xu, Qing-Song (2015) “Multi-step adaptive elastic-net: reducing false positives in high-dimensional variable selection.” Journal of Statistical Computation and Simulation, pp 1-11
17. Yan, X. and Su, X. G. (2005). “Testing for Qualitative Interaction”. Encyclopedia of Biopharmaceutical Statistics: Second Edition, Revised and Expanded Edition